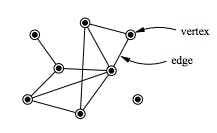
WHAT IS A NETWORK?
A network (or graph) G is a collection of nodes (or vertices) V connected by links (or edges) E. The network is denoted by G=(V,E)
Example of a network with 8 vertices (of which one is isolated) and 10 edges.
WHY ARE WE INTERESTED IN NETWORKS?
The study of networks is crucial for understanding the behavior of many systems of interest. These systems, such as the Internet, human societies, and others, are composed of individual parts or components that are linked together in some way. The nature of these connections or interactions is a crucial aspect of these systems that can have a significant impact on their behavior.
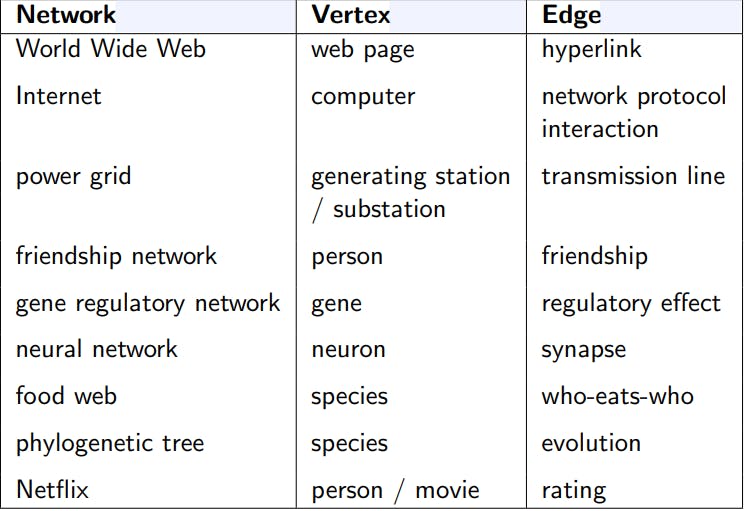
Example of networks.
Representing these systems as networks, which are simplified representations capturing only the basics of connection patterns can help to understand the structure and behavior of the corresponding systems.
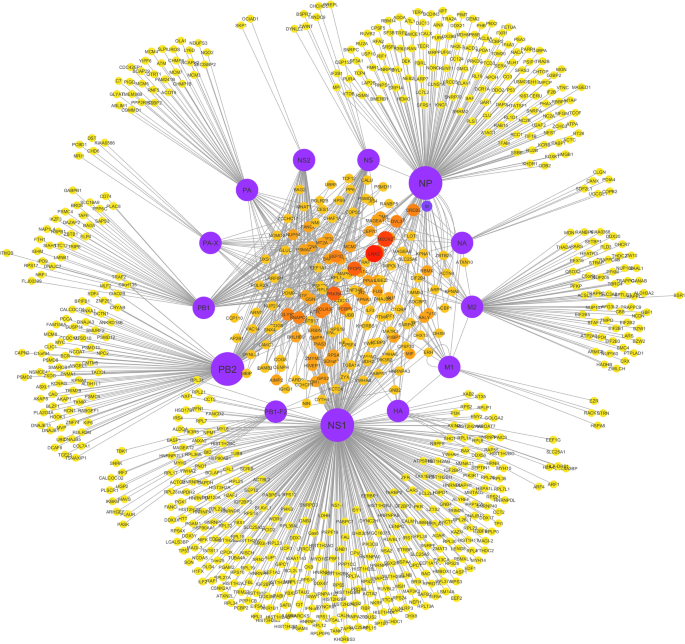
Protein-protein interaction network of Influenza.
Networks help to model and analyze complex systems, including communication networks, transportation systems, social networks, and biological networks, among others. The study of network structure is important for understanding how data is transported over the Internet, how opinions are formed in human societies, and other phenomena. By understanding the structure of networks, we can gain a deeper understanding of the behavior of the corresponding systems.
TYPES OF GRAPHS
Undirected Graphs: Undirected graphs are characterized by edges that lack directionality, representing a mutual connection between nodes. The edges in an undirected graph signify a two-way relationship, allowing movement in either direction along the edge.
Directed Graphs: Directed graphs, also known as directed networks or digraphs, are networks where the edges have a direction, indicating the flow of connections from one node to another. In a directed graph, edges are represented by arrows pointing from the source to the node destination, indicating the direction of the connection.
Weighted Graphs: Weighted graphs, also known as labeled graphs are graphs in which each edge has a weight or cost associated with it. The weight represents the strength, importance, or cost of the connection between two nodes.

Diagrammatic representation of different types of graphs.
QUANTITATIVE MEASURES OF NETWORKS
Quantitative measures are used to describe and analyze the structure and behaviour of networks. Here are some common quantitative measures in network science:
Connected Components: This is a measure of the number of connected subgraphs within a network. In a connected graph, all nodes are reachable from any other node, whereas, in a disconnected graph, there are multiple separate subgraphs.
The number of connected components in a graph can provide insight into the structure of the network and its robustness to failure or disconnections.
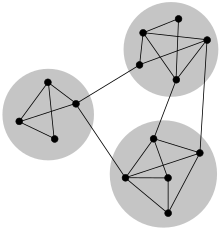
Connected components in a graph
Edge Density: Edge density or connectance is a measure of the number of edges in a network compared to the total number of possible edges.
$$\rho = \frac{m}{n\choose 2}$$
where |V| = n, |E| = m
Edge density provides an indication of how densely connected a network is, and can provide information about the sparsity or cliquishness of the network.
Degree: The degree (k) of a node refers to the number of edges connected to that node.
In an undirected graph, the degree of a node is simply the number of edges the node has.
In a directed graph, the degree is often split into two different measures:
in-degree, which is the number of edges that are pointing towards the node, and out-degree, which is the number of edges that are pointing away from the node.
The degree of a node gives a rough indication of its importance or centrality in the network, with nodes having high degrees often being considered more important or central.
Diameter and Average Path Length: The diameter of a network is the largest distance between any two nodes in the network.
$$diameter = \underset{i, j \in V}{max} d_{ij}$$
$$where \, d_{ij} \, denotes \, the \, length of the geodesic path or shortest path) between node i and j.$$
The average path length is the average distance between any two nodes in the network:
$$average \, path \, length = \frac{1}{n\choose2} \underset{i \le j}{\sum} d_{ij}$$
These measures give insight into the overall connectedness of a network and the efficiency of information transfer between nodes.
Modularity: This is a measure of the structure of a network that quantifies the extent to which a network can be divided into groups or communities of nodes that are more densely connected than they are to the rest of the network. A high value of modularity indicates that the network has a strong community structure, while a low value indicates that the network is not well structured and that there are few or no meaningful communities.
$$\frac{1}{2m} \sum_{i, j} (A_{i, j} - \frac{k_i k_j}{2m}) \delta(t_i, t_j) \in[-1, 1]$$
$$where \, t_i \, is type of node i and \delta(a, b) = 1 if a = b and 0 otherwise$$
$$the adjacency matrix A_{ij} = \begin{cases} 1, if (i, j) \in E \ and 0 otherwise \end{cases}$$
The adjacency matrix is a matrix of size n x n (where n = |V|).
QUESTIONS NETWORK ANALYSIS CAN HELP ANSWER
Network analysis can help answer a wide range of questions, including:
Connectivity: What is the structure of the network, and are there any isolated components or bottlenecks?
Centrality: What are the most important nodes in the network? What nodes are mostly involved in the transfer of information, resources, or signals between other nodes in the network? What node is the closest to other nodes in the network?
Community Structure: What are the underlying communities or clusters in the network, and how are they related to each other?
Influence Propagation: How does information or influence spread through the network, and what factors determine the speed and efficiency of propagation?
Network Evolution: How does the network change over time, and what are the mechanisms and drivers of change?
Robustness: How robust is the network to failure or attack, and what are the key nodes or links that are critical for network stability?
Link Prediction: Can we predict future connections or links in the network based on the current network structure and node attributes? and so on.